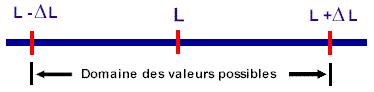Les incertitudes Cliquez ici pour la version Word du présent document Introduction La mesure Lorsque nous prenons une mesure, nous ne pouvons pas prétendre que celle-ci correspond à la valeur exacte de la grandeur mesurée. Que la mesure soit celle d'une longueur, d'une masse, d'un volume ou d'un intervalle de temps, nous devons inévitablement nous rendre à l'évidence que notre mesure est plus ou moins proche de la réalité. L'erreur L'erreur, c'est l'écart entre la mesure et la valeur exacte. Puisque la valeur exacte est souvent inaccessible, l'erreur est inconnue. L'incertitude absolue L'incertitude absolue est une estimation de l'erreur que fait l'expérimentateur. L'incertitude absolue est l'écart maximum possible entre la mesure et la valeur exacte. La mesure et son incertitude absolue constituent un domaine de valeurs possibles à l'intérieur duquel se trouve la valeur exacte. L : la mesure d'une longueur La valeur exacte se trouverait donc à l'intérieur du
domaine délimité par
L'incertitude absolue dépend de plusieurs facteurs ; la précision de l'appareil de mesure, les conditions dans lesquelles se prend la mesure, l'habileté de l'expérimentateur, etc. Estimer correctement l'incertitude associée à une mesure exige une bonne part de jugement et d'expérience. L'incertitude absolue s'exprime généralement avec un seul chiffre en utilisant les mêmes unités que celles associées à la mesure. Exemple : 23,4 ± 0,5 cm Puisque l'incertitude est estimée à 5 mm, la mesure est arrondie (si nécessaire) au millimètre le plus proche. L'incertitude relative L'incertitude relative est le rapport entre l'incertitude absolue et la mesure. Ce rapport est habituellement exprimé en pourcentage. Exemple : 23,4 ± 0,5 cm pourrait aussi s'écrire 23,4 ± 2% L'incertitude relative permet de comparer la précision de différentes mesures. La mesure la plus précise est celle dont l'incertitude relative est la plus faible. Les chiffres significatifs Lorsqu'on exprime une mesure directe ou le résultat
d'un calcul, l'incertitude absolue associée au résultat est exprimée avec un seul
chiffre significatif. La mesure ou le résultat du calcul sera donc arrondi afin de
ne comporter qu'un seul chiffre incertain. Exemple : le résultat d'un calcul donne 23,456 ± 0,234 cm. Ce résultat devrait s'écrire, en tenant compte des chiffres significatifs, 23,5 ± 0,2 cm. L'incertitude à été arrondie pour ne comporter qu'un seul chiffre significatif et le résultat à été arrondi pour ne comporter qu'un seul chiffre incertain (le résultat comporte donc trois chiffres significatifs). Dans les sections qui suivent, nous regarderons comment se répercutent les incertitudes lors des calculs. |