| Cinématique L'accélération résultante |
| Lorsqu'une particule se déplace sur une trajectoire courbe, sa vitesse peut varier en grandeur et en direction. Si seulement l'orientation de la vitesse change, l'accélération est centripète car elle est dirigée vers le centre de courbure (voir la capsule sur l'accélération centripète). |
Pour revoir l'animation, actualisez ou rechargez la page.
| La figure précédente représente une particule dont la
grandeur de la vitesse augmente sur sa trajectoire circulaire. L'accélération
résultante de cette particule est orientée dans le même sens que le vecteur variation
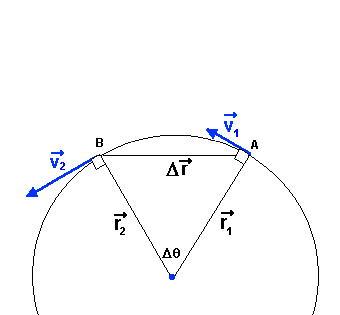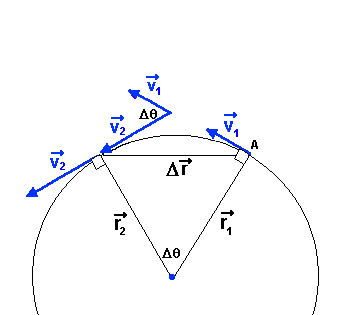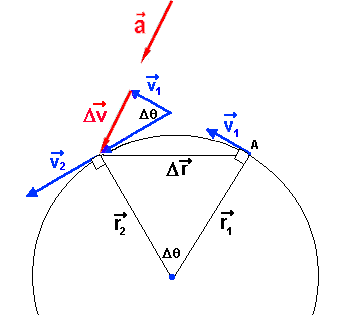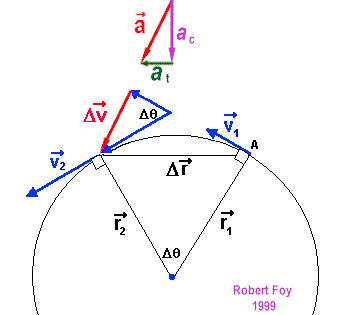
de vitesse (ces deux vecteurs sont indiqués en rouge sur la figure).Cette
accélération résultante a possède deux composantes. La composante radiale
(ou centripète) ac est responsable du changement
d'orientation du vecteur vitesse. ac= v2/r Lorsque la grandeur de la vitesse varie, il y a aussi une composante tangentielle à l'accélération. Cette composante est tangente à la trajectoire de la particule. Si cette composante est dirigée dans le même sens que la vitesse c'est que le module de la vitesse augmente. Si elle est dirigée dans le sens contraire à la vitesse c'est que le module de la vitesse diminue. La composante tangentielle est donnée par le taux de variation de la grandeur de la vitesse. at = dv/dt Ces deux composantes étant toujours perpendiculaires, la grandeur de l'accélération résultante est donnée par ; a = (ac2 + at2)1/2 Question :Une automobile décrit un cercle de 50 m de rayon. Au moment où sa vitesse est de 20 m/s vers le Nord, son accélération résultante est dirigée à 20° au Sud de l'Est. (a) Déterminez l'accélération centripète de la voiture. (b) Déterminez l'accélération tangentielle de la voiture. (c) Déterminez la grandeur de l'accélération résultante. (d) La vitesse de la voiture augmente-t-elle ? Réponses : (a) 8,0 m/s2 (vers
l'Est) |