| Cinématique L'accélération centripète |
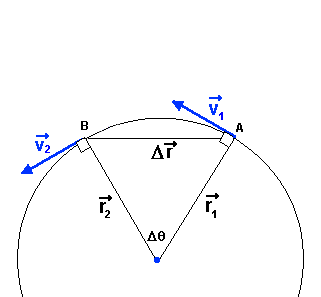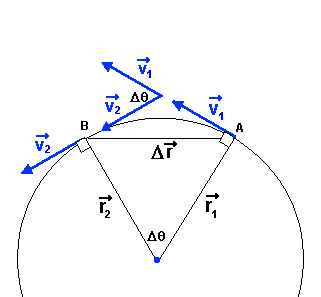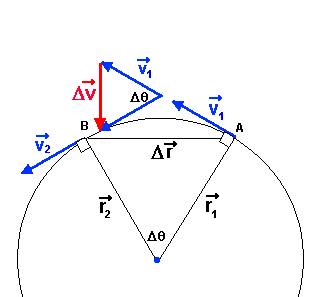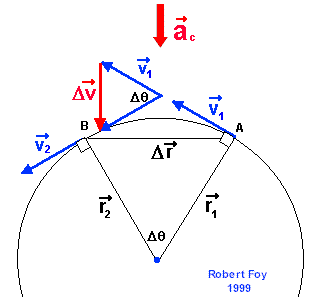
| Le mouvement circulaire uniforme met en évidence l'accélération associée au changement d'orientation du vecteur vitesse. Dans ce type de mouvement, la grandeur de la vitesse de la particule demeure constante mais l'orientation de celle-ci, tangente à la trajectoire, varie continuellement. La figure suivante montre la vitesse de la particule à deux instants (points A et B). L'accélération de la particule est orientée dans le même sens que le vecteur variation de vitesse (ces deux vecteurs sont indiqués en rouge sur la figure). |
Pour revoir l'animation, actualisez ou rechargez la page.
| Comme la
vitesse de la particule est toujours perpendiculaire à son vecteur position, l'angle Dq entre les vecteurs vitesse
est le même que celui entre les vecteurs position. Nous avons donc deux
triangles isocèles semblables car v1= v2 = v et r1 = r2 = r. En comparant ces deux triangles nous avons que ; Dr/r = Dv/v puisque la longueur d'arc Ds (entre A et B) et la grandeur du déplacement Dr (la corde entre A et B) tendent vers la même valeur si l'intervalle de temps choisi est très court, nous pouvons remplacer Dr par Ds = vDt . vDt/r = Dv/v Comme la grandeur de l'accélération instantanée est donnée par le rapport Dv/Dt lorsque Dt est infiniment petit, sa grandeur (ou module) est donnée par : ac= v2/r. Cette accélération (appelée centripète) est toujours orientée vers le centre de la trajectoire circulaire de la particule. Question :La navette spatiale décrit autour de la terre une trajectoire circulaire à environ 300 km d'altitude. Si la grandeur de sa vitesse est de 28 500 km/h, quelle est son accélération centripète ? Réponse : |