Analogies entre les équations de la rotation et de la translation
Cliquez ici pour la version Word de cette page
|
La cinématique |
||
| translation | rotation | |
| position: | x (m) | q (thêta) (rad) |
| vitesse: | vx (m/s) | wz (oméga) (rad/s) |
| accélération: | ax (m/s2) | az (alpha) (rad/s2) |
| translation | rotation |
| x = xo + vxo t + 1/2 ax t2 | q = qo + wzo t + 1/2 a z t2 |
| vx = vxo + ax t | w z = wzo + a z t |
| vx2 = vxo2 + 2axDx | wz 2 = wzo2 + 2az Dq |
|
La dynamique |
|
| S Fx = m ax | S tz = I az |
|
L'énergie cinétique |
|
| K = 1/2 mv 2 | K = 1/2 Iw 2 |
|
Quantité de mouvement et moment cinétique |
|
| px = m vx | Lz = I wz |
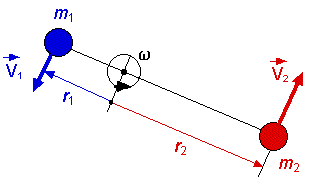
Le moment d'inertie d'un système composé de plusieurs masses ponctuelles
|
La masse inertielle m d'une particule est la mesure de son inertie de translation. Elle représente l'opposition qu'offre un corps à voir changer son état de mouvement de translation. En rotation, c'est le moment d'inertie I d'un système qui représente la mesure de l'opposition qu'offre ce système à voir changer son état de mouvement de rotation autour d'un axe (accélération angulaire).
I = S
mi
ri2
|
Quelques moments d'inertie (distribution de masse uniforme)
| Le tableau suivant donne l'expression du moment d'inertie de quelques solides, de masse totale M, par rapport à un axe passant par leur centre de masse. Pour le cylindre et l'anneau, cet axe est perpendiculaire à leur rayon. |

|
2MR2/5 |
2MR2/3 |
MR2/2 |
MR2 |
Le moment d'une force (Le moment de force)
|
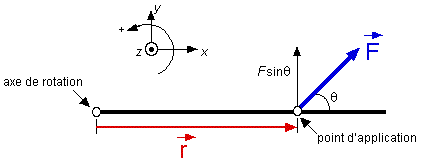
Le moment d'une force, c'est sa tendance à faire tourner. Pour faire tourner un corps rigide autour d'un axe fixe, il faut que soit appliquée une force exerçant un moment de force t (tau) par rapport à cet axe.
| tz | = r F sinq |