Cette page explique les différentes opérations à effectuer dans EXCEL pour déterminer l'incertitude absolue sur la pente d'un graphique. Par deux exemples, les différentes étapes nécessaires seront expliquées.

EXEMPLE A : Incertitudes en ordonnée seulement

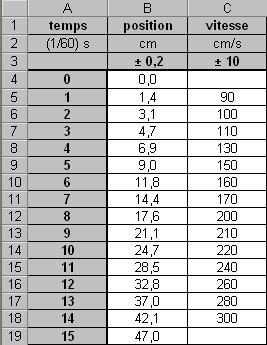
1. À partir du tableau ci-contre, le graphique suivant a été tracé par Excel. Il s'agit du graphique de la vitesse en fonction du temps d'une bille d'acier en chute libre. Les colonnes A et C ont été sélectionnées. Dans le but d'ajouter des données au graphique pour tracer les droites de pentes maximale et minimale, les colonnes sélectionnées auront toujours une étendue qui correspond aux temps (coordonnées en abscisse) compris de 0 à 15 soixantièmes de seconde. Une courbe de tendance a été tracée et l'équation de la droite a été affichée. L'incertitude absolue en ordonnée a été ajoutée (± 10 cm/s). Le motif par défaut d'EXCEL a été utilisé pour les barres d'incertitude.

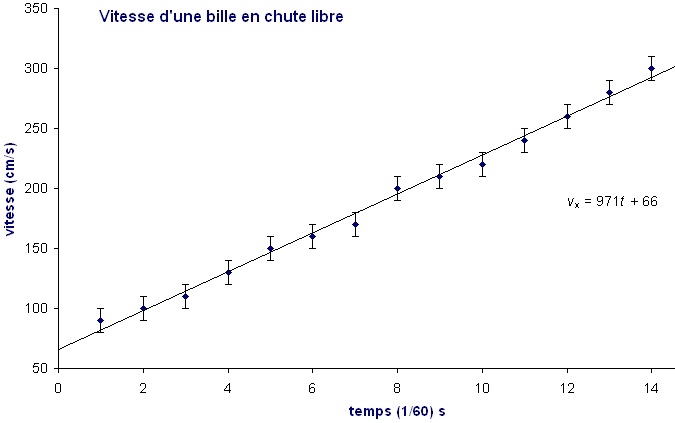
Il faut maintenant déterminer les coordonnées des point situés sur la droite tracée par EXCEL qui serviront aux calculs des pentes maximal et minimal possibles. Ces deux points sont choisis légèrement à l'extérieur du domaine expérimental étudié. Comme ce domaine s'étend de t = 1 à t = 14 soixantièmes de seconde, les points servant aux calculs des pentes extrêmes seront sur la droite à t = 0 et t = 15 soixantièmes de secondes. En utilisant l'équation de la droite, ces points sont les suivants : 66 cm/s à t  =  0 (l'ordonnée à l'origine) et 308 cm/s à t  =  15 soixantièmes de seconde.

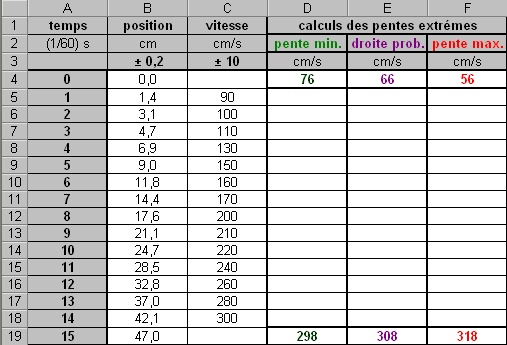
2. Nous devons associer à ces deux points situés sur la droite, la même incertitude absolue que le point expérimental le plus proche. 3. Dans le tableau ci-contre, des colonnes ont été ajoutées pour indiquer à EXCEL les séries de données à ajouter au graphique précédent. Pour tracer les droites de pentes extrêmes, les points 76 et 298 cm/s serviront pour tracer la droite de pente minimale et les points 56 et 319 cm/s serviront pour tracer la droite de pente maximale.

4. En ajoutant successivement les données des colonnes D et F au graphique précédent, nous obtenons le graphique final suivant :

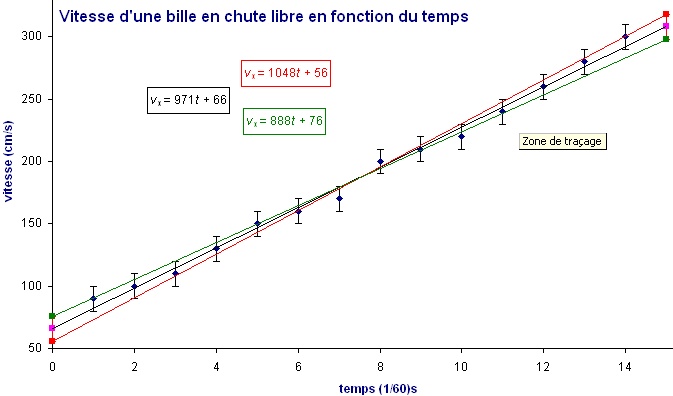
Les trois équations affichées sur le graphique permettent d’écrire que la pente du graphique est (970 ± 80) m/s²

EXEMPLE B : Incertitudes en ordonnée et en abscisse

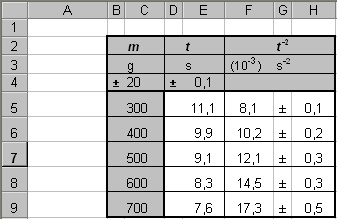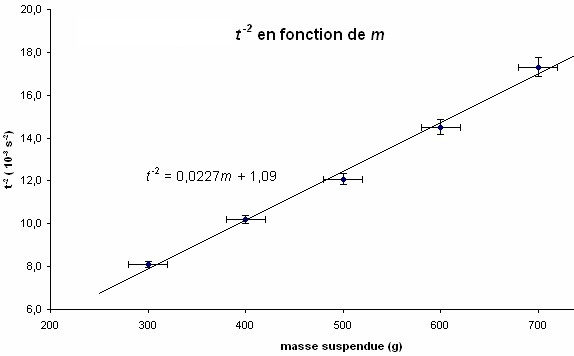
1. À partir du tableau ci-contre, le graphique suivant a été tracé par EXCEL. Il s'agit du graphique de t -2 en fonction de la masse m. Les colonnes C et F ont été sélectionnées. Notez que l'incertitude en abscisse est constante ( ± 20 g), et que l'incertitude en ordonnée varie d'un résultat à l'autre dans la colonne H. Une courbe de tendance a été tracée et l'équation de la droite a été affichée. Les coordonnées des points situés sur la droite tracée par EXCEL qui serviront aux calculs pour déterminer les valeurs des pentes maximale et minimale possibles seront les valeurs situées à 250 et 750 g en abscisse.

Les coordonnées en ordonnée sont calculées en utilisant l'équation de la droite tracée par Excel. Pour m = 250 g, t ^-2 = 6,77 X 10^-3 s^-2 et pour m = 750 g, t ^-2 = 18,12 X 10^-3 s^-2. Puisque ce sont des résultats provenant d'un calcul et non des résultats expérimentaux, il est important de ne pas trop arrondir ces derniers.

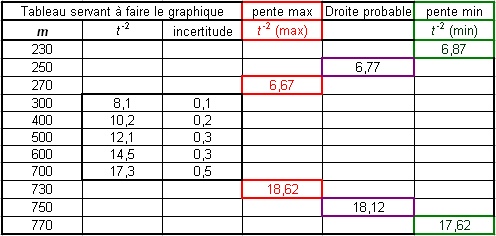
2. Nous devons associer à ces deux points situés sur la droite, la même incertitude absolue que le point expérimental le plus proche. Remarquez qu'il faut tenir compte de l'incertitude en abscisse. 3. Dans le tableau ci-contre, des colonnes ont été ajoutées pour indiquer à EXCEL les séries de données à ajouter au graphique précédent.

4. En ajoutant successivement les données des colonnes associées aux pentes extrêmes au graphique précédent, nous obtenons le graphique final suivant :

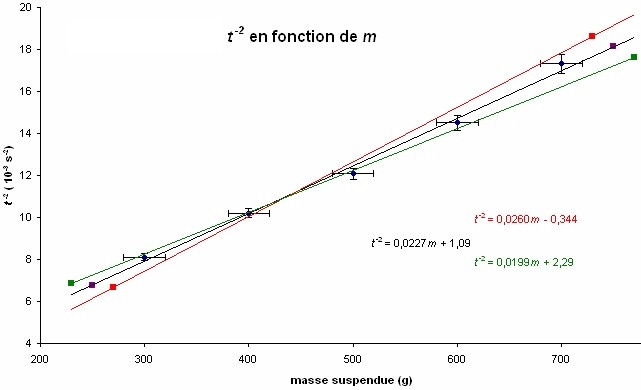
Les trois équations affichées sur le graphique permettent d’écrire que la pente du graphique est 
(0,023 ± 0,003) X 10^-3 s^-2 g^-1

Retour au menu principal