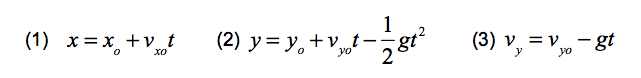| 4.1 Le mouvement des projectiles - théorie |
|
Les équations (1) et (2) (appelées paramétriques) décrivent l'évolution des coordonnées de position x et y d'une particule effectuant une trajectoire dans un plan vertical sous l'effet de la force gravitationnelle. Ces équations sont les mêmes que celles utilisées au chapitre 3. Ces équations sont valables si l'axe x est horizontal et l'axe y vertical et orienté vers le haut. La composante en x de la vitesse est constante tandis que la composante en y varie de la même façon que lors d'un mouvement de chute libre verticale. Les composantes, selon les axes x et y, de la vitesse initiale s'exprime en fonction du module de celle-ci ainsi que de son orientation (angle conventionnel).
L'équation de la trajectoire L'équation de la trajectoire de la particule y = f (x) s'obtient en éliminant le temps t des équations paramétriques x = f (t) et y = f (t).
Je vous propose une méthode de résolution pour les exercices de cette section. Cliquez ici pour consulter la capsule sur le mouvement parabolique La physique en action |