| 3.1 La cinématique
à une dimension - théorie |
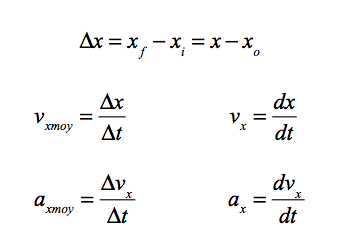
|
Ces équations constituent les définitions de base de la
cinématique à une dimension.

Vitesse moyenne et vitesse
instantanée
|
|
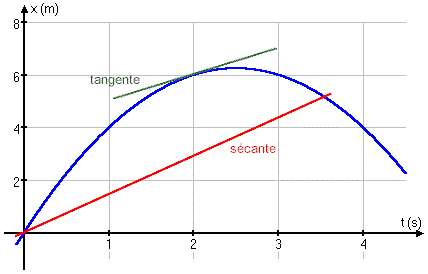
La vitesse moyenne correspond à la pente de
la sécante entre deux points sur le graphique de la position en fonction
du temps (entre t = 0 et t = 3,5 s sur le graphique). La vitesse instantanée correspond à la pente de la tangente en
un point (à t = 2,0 s sur le graphique) du graphique de la position en fonction du
temps. La pente d'une droite située sur un graphique de position en
fonction du temps s'exprime habituellement en m/s. La pente de la tangente
en un point correspond à la
dérivée en ce point de la fonction de position.

Accélération moyenne et
accélération instantanée
|
|
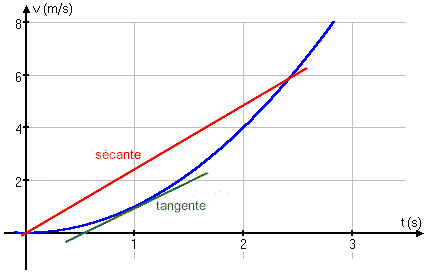
L'accélération moyenne correspond à la
pente de la sécante entre deux points sur le graphique de la vitesse en
fonction du temps (entre t = 0 et t = 2,5 s sur le
graphique). L'accélération instantanée correspond à la pente de
la tangente en un point (à t = 1,0 s sur le graphique) du graphique de la vitesse en fonction du
temps. La pente d'une droite située sur un graphique de vitesse en
fonction du temps s'exprime habituellement en m/s2. La pente de
la tangente en un point correspond à la
dérivée en ce point de la fonction de vitesse.

Utilisation des aires
|
|
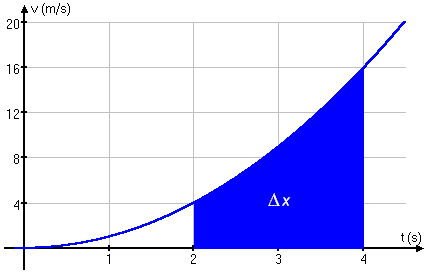
L'aire comprise sous la fonction de vitesse
(graphique de la vitesse en fonction du temps) pour un intervalle de temps
donné ( entre t = 2 s et t = 4 s sur le graphique) correspond au déplacement effectué.
L'aire, sur un graphique de vitesse en fonction du temps, possède des
unités de déplacement.

|
|