Solution E11 chapitre 9

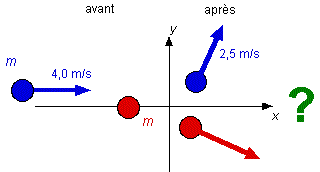
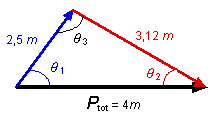
Puisqu'il s'agit d'une collision élastique, l'énergie cinétique totale sera conservée. Les deux masses étant identiques nous pouvons trouver la vitesse inconnue.

K_tot = K' _tot

¹/₂ m v₁ ² =  ¹/₂ m v'₁ ²  +  ¹/₂ m v'₂ ²

Dans l'équation précédente  v₁ = 4,0 m/s et v'₁ = 2,5 m/s, comme les masses s'annulent dans cette équation, il ne reste plus qu'à trouver la vitesse v'₂ .Cette vitesse a un module de 3,12 m/s.

Pour trouver l'orientation de chacune des vitesses il faut maintenant considérer la quantité de mouvement (toujours conservée lors des différents types de collisions). La quantité de mouvement initiale a un module P_tot = 4m et est dirigée dans le sens positif de l'axe x. La somme vectorielle des quantités de mouvement des deux masses après la collision doit donc être égale à cette quantité de mouvement initiale.

En utilisant la loi des cosinus on obtient que l'angle q₃ est de 90° (ceci était prévisible). On trouve par la suite les angles q₁ = 51,3° et  q₂ = 38,7°.

Une autre solution est possible. Si la masse bleue est déviée vers le bas (sous l'axe x ), la deuxième masse serait déviée vers le haut. Les modules des vitesses étant les mêmes, les angles seraient aussi les mêmes (mais mesurés en-dessus de l'axe x pour q₁  puis au-dessus de l'axe pour q₂ )

On peut remarquer que lors d'une collision élastique entre deux masses de même valeur (l'une étant initialement immobile), l'angle entre les vitesses des deux masses après la collision est toujours de 90° (les bons joueur de billarde le savent).