Solution E3 chapitre 4

Voici le schéma de la situation initiale.

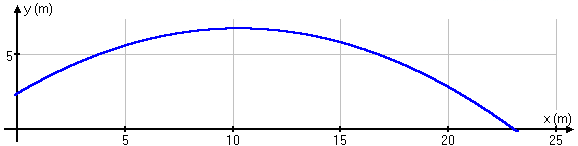
(a) Comme la grandeur de la vitesse initiale est inconnue, les équations paramétriques peuvent s'écrire

x = (v_ocos40°) t   (1)

y = 2,40 + (v_osin40°) t - 4,9 t²   (2)

Comme les conditions initiales ne sont pas toutes connues, il faut se servir de conditions ultérieures. Nous savons que le poids arrive au sol (y = 0) lorsque x = 23,1 m. En remplaçant ces conditions dans les équations précédentes on obtient

 (v_ocos40°) t  = 23,1

2,40 + (v_osin40°) t - 4,9 t² = 0

Nous avons maintenant deux équations dans lesquelles se trouvent deux inconnus, v_o et t. En solutionnant on obtient que v_o = 14,3 m/s et t = 2,11 s.

(b) La composante verticale de la vitesse est donnée par

v_y = 14,3sin40° - 9,8 t   (3)

on trouve que v_y = 0 à t = 0,938 s, à cet instant on peut calculer que y = 6,70 m (c'est la hauteur maximale atteinte).

(c) En utilisant l'équation (3), on trouve que la composante verticale de la vitesse est de - 11,5 m/s lorsque le poids arrive au sol (à t = 2,11 s). Comme la composante horizontale de la vitesse à cet instant, comme à tout autre instant, est de 11,0 m/s, on peut calculer la grandeur ainsi que l'orientation de la vitesse du poids lorsqu'il entre en contact avec le sol.

Remarque: L'équation de la trajectoire est

y = - 0,0408x² + 0,838x + 2,4

En voici le tracé