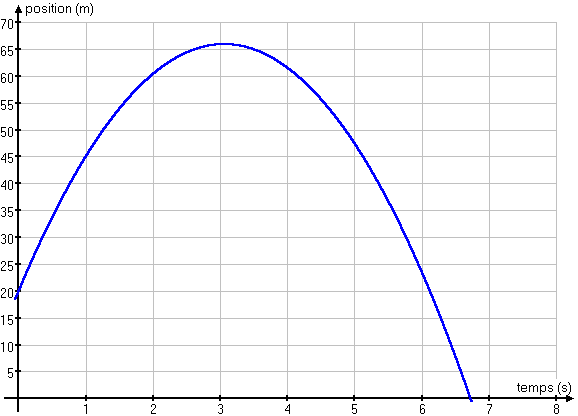
Solution E13 chapitre 3

Cet exercice est solutionné en utilisant un axe y orienté verticalement vers le haut.

(a) En utilisant l'équation de la position en fonction du temps on obtient qu'à t = 2,0 s, la balle est à 60,4 m de hauteur.

(b) L'équation de la vitesse en fonction du temps nous donne une vitesse de + 10,4 m/s (la balle monte toujours)

(c) La vitesse de la balle est nulle à t = 3,06 s. La position maximale de la balle est donc de 65,9 m.

(d) En utilisant l'équation de la position en fonction du temps, la balle atteint y = 50 m à t = 1,26 s puis à t = 4,86 s, ces temps sont symétriques par rapport au temps de passage au sommet (il faut résoudre une équation quadratique).

(e) L'équation de la vitesse en fonction du temps nous donne une vitesse de + 17,7 m/s à t = 1,26 s puis - 17,7 m/s à t = 4,86 s.

(f) En utilisant l'équation de la position en fonction du temps, y = 0 à t = 6,73 s , la solution t = - 0,61 s est à rejeter car elle correspond au passé (il faut résoudre une équation quadratique).

Graphique de la position de la balle en fonction du temps.

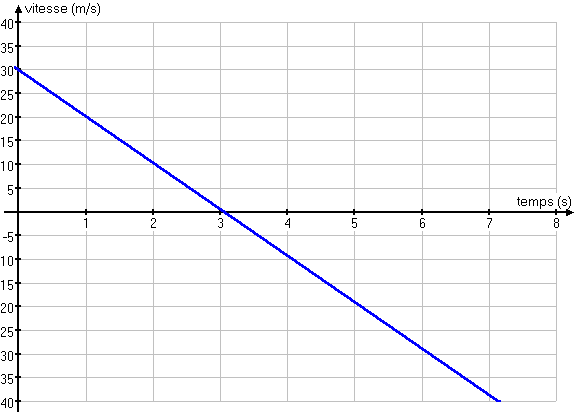
Le Graphique de la vitesse de la balle en fonction du temps.