Solution E4 chapitre 10

Le rouage d'entraînement de la bicyclette de John Howard

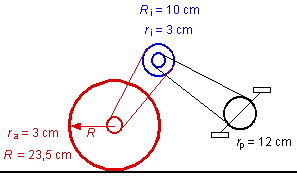
La vitesse de la bicyclette s'exprime en fonction de la vitesse angulaire de la roue arrière et du rayon de celle-ci

(1) v = w_R R

Comme nous avons le rayon de la roue arrière ainsi que la vitesse de la bicyclette (152 Mph = 68,0 m/s), nous pouvons calculer sa vitesse angulaire (289 rad/s = 46,0 tours/s). Le pédalier tourne certainement beaucoup moins vite.

Partons du pédalier. La vitesse tangentielle d'un maillon de la chaîne reliant le pédalier au plateau intermédiaire (bleu) doit être la même à l'extrémité du pédalier que sur le petit pignon du plateau intermédiaire.

(2) w_p r_p = w_i r _i

L'équation précédente nous permet d'établir que le plateau intermédiaire tourne quatre fois plus vite que le pédalier. Le plateau intermédiaire entraîne le pignon de la roue arrière. Tout comme le pignon de rayon r _i est solidaire du plateau intermédiaire (ils ont la même vitesse angulaire w_i) le pignon arrière a la même vitesse angulaire que la roue arrière w_R. La vitesse tangentielle d'un maillon de la chaîne reliant le plateau intermédiaire à la roue arrière doit être la même à l'extrémité du plateau intermédiaire que sur le pignon de la roue arrière.

(3) w_i R _i = w_R r_a

L'équation précédente nous permet d'établir que la roue arrière tourne 3,33 fois plus vite que le plateau intermédiaire (qui tourne déjà quatre fois plus rapidement que le pédalier). Ce rouage d'entraînement permet de multiplier par 13,3 la vitesse de rotation du pédalier. Quel est le rapport maximal que permet votre bicyclette?

En combinant les équations (1), (2) et (3), on trouve une vitesse de rotation de 207 tours/min pour le pédalier.