Formules

Formules

Théorème de Pythagore

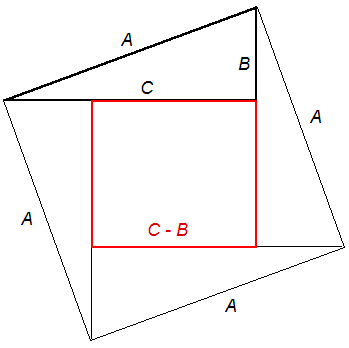La figure ci-contre permet de démontrer le théorème de Pythagore.

La figure extérieure possède une aire égale à A² . Par symétrie, cette aire est équivalente à la somme de l'aire du carré de côté C-B plus quatre fois l'aire du triangle rectangle d'hypoténuse C et de côtés A et B.

A² = (B-C)² + 4(BC)/2

A² = B² + C² - 2BC + 2BC

A² = B² + C²

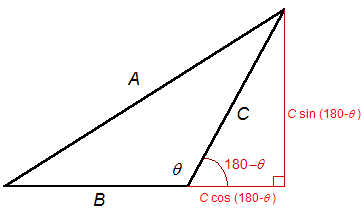
Lois des cosinus (triangle quelconque de côtés A, B et C)

En appliquant le théorème de Pythagore au triangle rectangle d'hypoténuse A et de côtés de longueur (B + Ccos(180-q )) et Csin(180-q ) on obtient :

A² = (B + Ccos(180-q )) ² + (Csin(180-q ))²

A² = B² + C²cos² (180-q ) + 2BCcos (180-q ) + C²sin²(180-q )

A² = B² + C²cos² (180-q ) + C²sin²(180-q ) + 2BCcos (180-q )

A² = B² + C²(cos² (180-q ) + sin²(180-q )) + 2BCcos (180-q )

A² = B² + C² + 2BCcos (180-q )

Finalement (puisque cos (180-q) = - cosq) :

A² = B² + C² - 2BCcosq

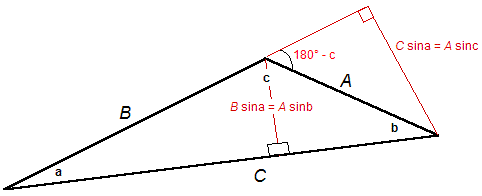
Lois des sinus (triangle quelconque de côtés A, B et C)

La figure précédente nous permet de voir que la hauteur du triangle est de Bsina ou Asinb (en considérant les deux triangles rectangle formés en traçant le hauteur du triangle). En prolongeant le côté de longueur B pour former un troisième triangle rectangle, il est possible de voir que Csina = Asinc (car sin (180 - c) = sinc.

On obtient finalement que pour un triangle quelconque :

A/sina = B/sinb = C/sinc