|
|
La
dynamique de translation (deuxième partie)
L'avion doit incliner ses ailes pour
effectuer un virage. Un corps en mouvement sur une trajectoire circulaire
doit être soumis à une force résultante ayant une composante dirigée
vers le centre de cette trajectoire. |
 E1. E1.
|
Au
curling, les bons joueurs sont très sensibles au frottement
cinétique entre leur pierre et la surface glacée. Si la pierre
quitte la main du joueur avec une vitesse initiale de 3 m/s et
que celle-ci s'immobilise 35 m plus loin, quelle est la valeur
du coefficient de frottement entre la pierre et la surface
glacée ?
Sur la
photo: trois membres de l'équipe canadienne,
championnes mondiales en 2008 |
 |
|
 E3. E3.
Un bloc
de 2,0 kg repose sur une surface horizontale. Les coefficients
de frottement statique et cinétique sont de 0,8 et 0,5 entre la
surface et le bloc.
(a) Quelle doit être la force minimale appliquée à 30° pour
mettre en mouvement le bloc ?
(b) Une fois le bloc en mouvement, quelle force doit être
appliquée pour permettre au bloc de se déplacer à vitesse
constante (la force est toujours orientée à 30°) ?
Indice
|
|
|
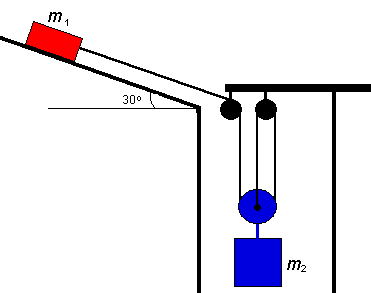
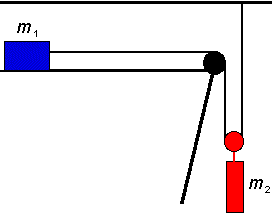
  E4. E4.
Un bloc de
masse m1 = 3 kg est relié à une masse
suspendue m2 = 2
kg par une corde de masse négligeable passant par une poulie fixe
(noire) ainsi que par une poulie mobile (rouge) solidaire de la
masse suspendue. Une extrémité de la corde est attachée au
plafond. Les coefficients de frottement statique et cinétique entre la surface
horizontale et le bloc sont de 0,25 et 0,2.
(a) Quelle doit être la tension minimale dans la corde pour
mettre en mouvement m1 ?
(b) Si le bloc m1 est maintenue immobile, quelle est
la tension dans la corde ?
(c) Si on relâche le bloc m1, quelle est l'accélération de chacune des
masses ?
(d) Quel est le module de la tension dans la corde ?
|
 |
|
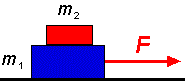
   E6. E6.
Sur un
bloc de masse m1 = 3 kg repose un
deuxième bloc de masse m2 = 2 kg. Les coefficients
de frottement statique et cinétique entre toutes les surfaces
sont respectivement de 0,35 et 0,2.
(a) Quelle est la plus grande valeur de F qui permet au
deux blocs d'avoir la même accélération ?
(b) Si F = 35 N, quelle est l'accélération
de chacun des blocs ?
Indice
|
 |
|
 E7. E7.
| Les pneus
des voitures de tourisme ordinaires permettent des coefficients de
frottement statique et cinétique de 0,95 et 0,7. À quelle vitesse maximale une telle
voiture peut-elle négocier, sans déraper, une courbe horizontale dont le rayon
est de 50 m.
|
|
  E9. E9.
Un pendule
conique est constitué d’une masse de 500 g placée à l’extrémité
d’une corde de 1,5 m de longueur. Si la masse décrit une
trajectoire circulaire de 50 cm de rayon dans un plan horizontal
déterminez;
(a) la tension dans la corde
(b) sa période de rotation
|
 |
|
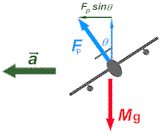
  E10.Un
avion filant à 350 km/h doit effectuer un virage de 2 km de rayon dans un plan horizontal. Quel
doit être l'angle d'inclinaison de ses ailes ? E10.Un
avion filant à 350 km/h doit effectuer un virage de 2 km de rayon dans un plan horizontal. Quel
doit être l'angle d'inclinaison de ses ailes ?
Indice
|
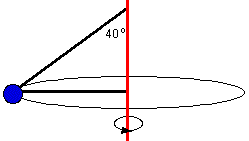
  E11. E11.
| Une masse
de 1 kg, attachée à l'aide de deux cordes, tourne autour d'un
arbre vertical à raison de 1 tour/s. Si la longueur de la corde
horizontale est de 65 cm, quelle est la tension dans celle-ci ? |
 |
|
 E12. E12.
Un
individu de 80 kg se tient debout sur le plancher d’un ascenseur.
Déterminez le poids apparent de l’individu
si :
(a) l’ascenseur accélère en montant à un taux de 2 m/s2
(b) l’ascenseur freine en descendant à un taux de 3 m/s2
(c) l’ascenseur freine en
montant à un taux de 2,5 m/s2
(d) l’ascenseur descend à une vitesse constante de 5 m/s
(e) l’ascenseur est en chute libre.
|
  E15. E15.
Une fusée quitte la surface de
la Terre avec une accélération de 7 m/s2
orientée à 70° par rapport à l'horizontale.
(a) Quel est le poids apparent
d'un astronaute de 80 kg prenant place dans cette fusée ?
(b) Quelle est l'orientation de la force résultante exercée par la
fusée sur l'astronaute ?
|
 E16. E16.
Un satellite géostationnaire
est un satellite qui paraît immobile dans le ciel car sa période de
révolution autour de la Terre est la même que la période de rotation de
la Terre autour de
son axe. À quelle distance du centre de la Terre doit-on placer un tel
satellite (la masse de la Terre est de 5,98 X 1024 kg) ?
|
 E17. E17.
La Terre met environ 365 jours pour effectuer une
révolution autour du Soleil. Si le rayon de l'orbite de la Terre est
d'environ 11 700 fois son propre diamètre (le rayon de la Terre est de 6 400 km), déterminez la masse du
Soleil.
|
|