Analyse d'une équation quadratique On rencontre souvent des équations quadratiques en
physique. Que ce soit pour décrire la position en fonction du temps d'une particule en
mouvement rectiligne uniformément accéléré, la coordonnée de position verticale d'une
particule en chute libre ou la trajectoire d'un projectile dans le plan cartésien, ces
différentes situations exigent que soient calculées les racines de la fonction (les
zéros) ou encore les coordonnées du sommet. |
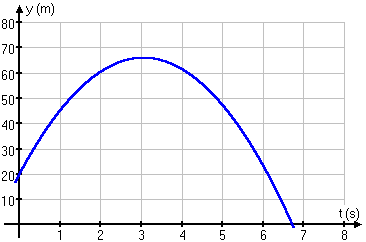 |
fig 1. Le graphique de la
coordonnée de position y en fonction du temps d'une particule lancée verticalement vers
le haut à une vitesse initiale de 30 m/s d'une hauteur de 20 m. y = - 4,9 t 2 + 30 t + 20 |
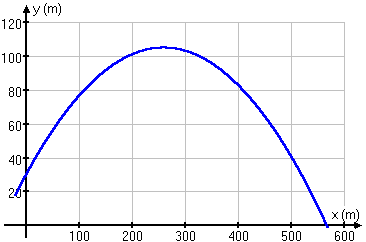
| fig 2. Le graphique de la
trajectoire d'une particule lancée à une vitesse initiale de 77 m/s orientée à 30°
par rapport à l'horizontale d'une hauteur de 30 m. y
= - 0,00111 x 2 + 0,577 x + 30 |
 |
Le programme suivant calcule les racines d'une équation quadratique ainsi que les coordonnées du sommet (utilisez le point plutôt que la virgule pour séparer les dixièmes des unités). y = ax 2 + bx + c |