| Cinématique Les équations du M.R.U.A. |
| Cette capsule a pour but de mettre en évidence les deux équations fondamentales de la cinématique à accélération constante. Le graphique suivant est celui de la vitesse en fonction du temps d'une particule décrivant un tel mouvement. |
pour revoir l'animation, rechargez ou actualisez la page.
| L'équation de la droite de ce graphique nous donne le comportement de la
vitesse en fonction du temps. vxo est
l'ordonnée à l'origine et ax l'accélération constante de cette
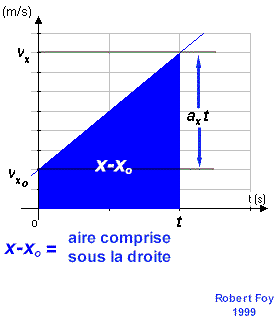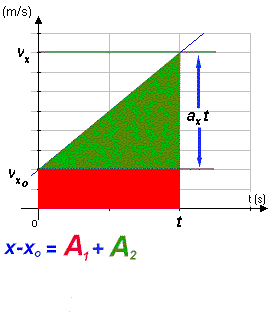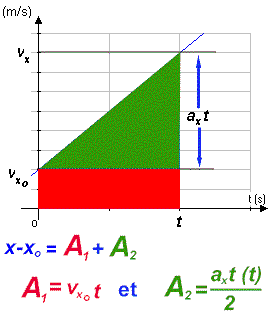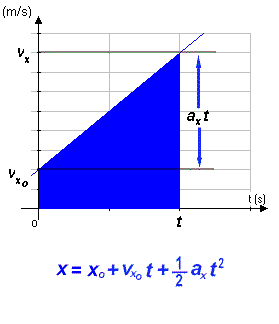
particule. vx = vxo + ax t L'animation montre les différentes étapes menant à l'équation de la position de la particule en fonction du temps. Le point de départ de la démonstration est que le déplacement d'une particule est donné par l'aire «sous la courbe» du graphique de sa vitesse en fonction du temps. Dans l'exemple illustré, l'aire est celle d'un trapèze. On peut considérer cette aire (en bleu) comme étant la somme des aires d'un rectangle (en rouge) et d'un triangle (en vert). L'équation finale... x = xo + vxo t + 1/2 ax t2 L'allure générale de cette fonction est la suivante :
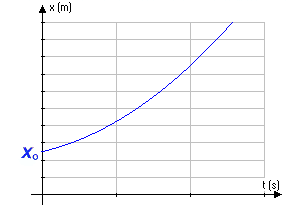
C'est une parabole dont l'ordonnée à l'origine correspond à la position initiale de la particule, dont la pente initiale correspond à la vitesse initiale de la particule. Si l'accélération de la particule est positive, la concavité de la parabole sera vers le haut (c'est le cas de notre exemple), sinon, elle sera vers le bas. Cette équation est valable même si l'accélération de la particule est nulle. Dans ce cas le graphique de la vitesse de la particule en fonction du temps serait une droite de pente nulle et sa position en fonction du temps serait donnée par l'équation : x = xo + vx t Dans l'équation précédente, vx représente la vitesse constante de la particule. On dit d'un tel mouvement qu'il est rectiligne uniforme (M.R.U.). L'équation précédente est celle d'une droite dont la pente est égale à vx . |