| Rotation Le moment d'inertie et l'énergie cinétique de rotation |
| La masse inertielle m d'une particule est la mesure
de son inertie de translation. Elle représente l'opposition qu'offre un
corps à voir changer son état de mouvement de translation. En rotation,
c'est le moment d'inertie I d'un système qui
représente la mesure de l'opposition qu'offre ce système à voir changer
son état de mouvement de rotation autour d'un axe (accélération
angulaire).
La figure suivante représente un système composé de deux particules m1 et m2 reliées entre elles par une tige de masse négligeable. L'ensemble est en rotation à une vitesse angulaire w (en rad/s) autour d'un axe situé à une distance r1 de m1 et r2 de m2. |
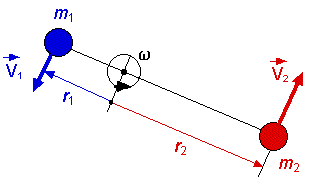
| Pour obtenir les propriétés du moment d'inertie du
système illustré ci-haut, considérons l'expression associée à son
énergie cinétique (énergie associée au mouvement). Pour des particules
possédant une vitesse de module v et une masse m,
l'énergie cinétique est donnée par l'expression K = ½ mv 2 L'énergie cinétique (de translation) du système illustré a donc pour expression K = ½ m1v12 + ½ m2v22 = Ktrans La vitesse de translation (sur une trajectoire circulaire) de chacune des deux masses est proportionnelle à la vitesse angulaire de rotation du système. L'énergie cinétique associée à la rotation du système est donc proportionnelle à w 2. Puisque v = w r, en remplaçant v1 et v2 par w r1 et w r2 dans l'équation précédente on obtient K = ½ m1( w r1 )2 + ½ m2 ( w r2 )2 K = ½ [ m1r12 + m2r22 ]w 2 Si la forme générale de l'expression de l'énergie cinétique de rotation est Krot = ½ Iw 2 L'expression du moment d'inertie du système est donc I = [ m1r12 + m2r22 ] Cette expression met en évidence l'importance qu'a la distribution de la masse autour de l'axe de rotation. Ainsi, plus la masse est proche de l'axe de rotation, plus l'inertie de rotation (le moment d'inertie) sera petite (et vice-versa bien sûr). De façon plus générale, pour un système composé de n particules (masses ponctuelles), le moment d'inertie est donné par I = S mi ri2 = m1r12 + m2r22 + ... + mnrn2 Dans cette expression, mi représente la masse de la ième particule et ri le rayon de la trajectoire circulaire qu'elle décrit lorsque le système est en rotation. Exercice : Réponse : Moments d'inertie et distributions
continues de masse
|
