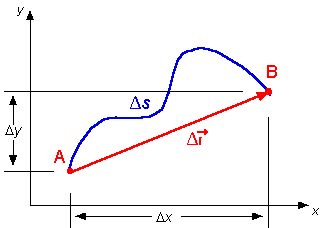
Le graphique précédent représente la trajectoire (en bleu) d'une particule s'étant déplacée du point A au point B. Ds représente la distance parcourue par la particule sur sa trajectoire. Ds, la distance parcourue, est une grandeur scalaire. Le rapport Ds/Dt  est la vitesse scalaire moyenne (Dt étant l'intervalle de temps nécessaire à la particule pour se rendre de A à B et ainsi parcourir la distance Ds). Dr représente le module du vecteur déplacement de la particule. Le vecteur déplacement (en rouge) a pour origine la position initiale de la particule et comme extrémité sa position finale. Le vecteur déplacement ne tient pas compte de la trajectoire emprunté par la particule pour se rendre de A vers  B. Le rapport Dr/Dt = v_moy correspond au module de la vitesse moyenne de la particule. La vitesse moyenne est une grandeur vectorielle orientée dans le même sens que le vecteur déplacement.

Dans l'espace à deux dimensions, Dx et Dy sont les composantes rectangulaires du vecteur déplacement. Les composantes rectangulaires du vecteur déplacement peuvent être négatives. La distance parcourue, Ds, est par contre toujours considérée positive.

Questions :
1. La distance parcourue peut-elle être plus petite 
que le module du vecteur déplacement ?
2. Si le vecteur déplacement est nul, la distance 
parcourue est-elle nécessairement nulle aussi ?
3. Dans quelle condition la distance parcourue est-elle égale à Dx ?

Réponses :
1. Non   2. Non   
3. Si le mouvement est rectiligne uniforme dans le sens positif de l'axe x.