1. La tension dans une corde de masse négligeable

Dans la plupart des situations faisant intervenir une corde reliant entre elles des composantes d'un système, nous pouvons considérer constante, donc unique, la valeur de la tension dans la corde. L'exemple qui suit vous en donne l'explication.

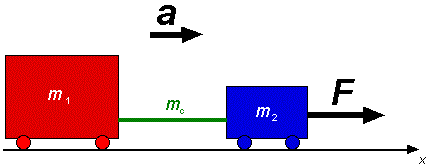
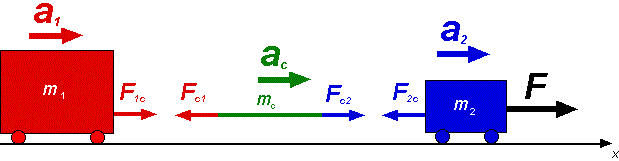
Deux chariots de masses m₁ et m₂ se déplacent vers la droite sous l'effet d'une force horizontale F appliquée sur le chariot de masse m₂. Les chariots sont reliés entre eux par une corde de masse m_c. Seules les forces dirigées selon l'axe x sont considérées. Les forces dirigées selon la verticale (les poids et forces normales appliquées sur les chariots) s'annulent mutuellement. Le frottement de roulement est considéré négligeable.

(a) Considérons les forces appliquées à l'ensemble.

(1)  SF_x = F =  ( m₁+ m₂ + m_c) a_x

Le schéma suivant montre les forces appliquées sur chacune des composantes du système.

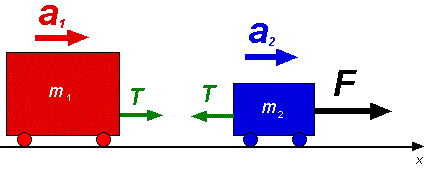
 L'équation précédente (1) implique que chacun des deux chariots ainsi que la corde ont la même accélération 

(2) a_x = a_x1 = a_x2 = a_xc

Considérons les forces horizontales exercées sur la corde

(3) SF_x = F_c2 -  F_c1 = m_c a_xc

dans cette équation,  F_c1 représente le module de la force exercée sur la corde par le chariot 1 et F_c2  le module de la force exercée sur la corde par le chariot 2, on peut en déduire que si la masse de la corde est nulle (négligeable) les forces exercées par les chariots 1 et 2 sur celle-ci, sont égales

F_c1 =  F_c2

Puisque d'après la troisième loi de Newton  F_c1  =  F_1c et  F_c2  =  F_2c , les modules de ces forces peuvent alors être remplacées par un seul symbole T, représentant le module de la tension dans la corde.

Dans le cas où la masse de la corde est négligeable, l'analyse des forces appliquées sur les composantes du système (ayant une masse) peut ce faire à partir du schéma suivant

Question : (a) Si m₁ = 3 kg, m₂ = 2 kg et F = 15 N.
Quelle est la grandeur de la tension dans la corde?
(b) Si m₁ = 2 kg, m₂ = 3 kg et F = 15 N. 
Quelle est alors la grandeur de la tension dans la corde?

Réponses : (a) 9,0 N  (b) 6,0 N

2. La tension dans une corde de masse M

(a) Corde suspendue à la verticale

Dans une corde suspendue à la verticale, la tension n'est pas la même sur toute sa longueur.

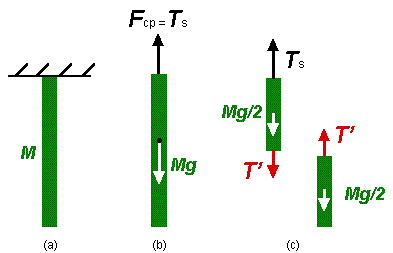
La figure (a) montre une corde de masse M suspendue au plafond. La figure (b) montre les forces qui s'exercent sut cette corde, son poids Mg ainsi que F_cp la force exercée sur la corde par le plafond. Ces deux forces doivent être de même grandeur si la corde est en équilibre. Selon la troisième loi de Newton, la force exercée sur la corde par le plafond doit être égale en grandeur à la force exercée sur le plafond par la corde, cette dernière correspond à la tension au sommet de la corde T_s. La figure (c) met en évidence les forces s'exerçant sur les parties supérieure et inférieure de la corde. En sectionnant ainsi la corde en deux parties, nous sommes en mesure de déterminer la valeur de la tension dans la corde au point de coupure. Si la masse de la corde est uniformément distribuée sur toute sa longueur, le tension T' à mi hauteur de la corde ne vaut que la moitié de la tension au sommet de la corde T_s . La tension dans la corde augmente lorsqu'on se déplace vers le sommet de celle-ci.

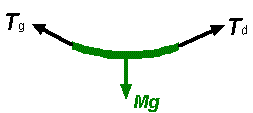
(b) Corde suspendue à l'horizontale

La figure précédente met en évidence le fait qu'une corde tendue entre deux points situés à une même hauteur ne peut pas être horizontale. Comme les tensions à droite et à gauche doivent avoir une composante verticale vers le haut, et puisque la tension s'exerce tangentiellement à la corde, celle-ci doit être recourbée vers le haut à ses extrémités. Plus la tension dans la corde sera grande, moins la courbure de celle-ci sera importante.