Soit un circuit RC où le condensateur est initialement chargé avec une source de potentiel Ɛ en fermant l'interrupteur présent. Le condensateur se charge presque instantanément et la charge alors emmagasinée par le condenstaeur est donnée par :

q_max = CƐ

q_max est la charge initiale de la phase de décharge, donc aussi la charge maximale (car elle ne fera que dimuner durant la décharge).

Le potentiel aux bornes du condensateur chargé est le même que la source, car il y est connecté directement.

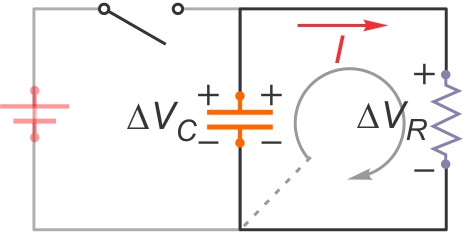
En ouvrfant l'interrupteur, la source est retirée du circuit et les électrons sur l'armature négative du condensateur peuvent alors circuler à travers la résistance pour rejoindre l'autre armature et annuler la charge. Le condensateur se « décharge à travers la résistance ».

La résistance empêche cette décharge de se faire instantanément, le courant ne pouvant être infini. La décharge se fera sur un certain temps, et en suivant une courbe précise...

Durant la décharge, on peut étudier l'équation de la maille unique du circuit, valide à tout instant :

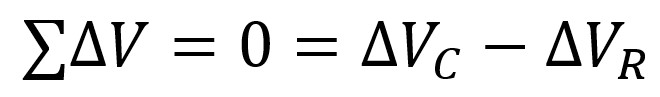
Selon l'équation de la capacité et la loi d'Ohm :

La structure de cette équation rend évident que si la charge q diminue, le courant I diminue également.

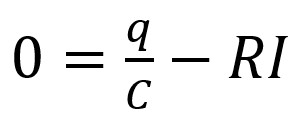Le courant I représente le taux de décroissance de la charge par rapport au temps. En équation :

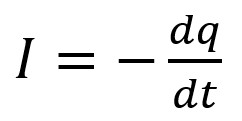
L'équation principale peut s'écrire :

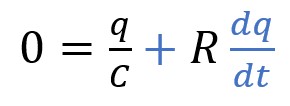
Si on réarrange l'expression pour isoler le rapport « dq/q » :

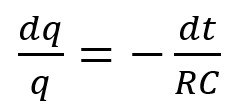
Si on intègre les deux termes de l'équation, on conserve l'égalité :

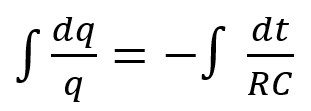
Le résultat de l'intégrale indéfinie, de chaque côté, génère une constante d'intégration qu'on peut réunir du côté droit dans une constante k :

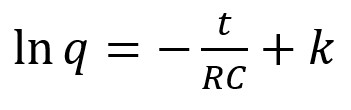
La constante d'intégration peut être déterminée à partir des conditions connues pour l'instant initial (t = 0) de la décharge :

À t = 0, la charge est à sa valeur initiale maximale, q = q_max.

On peut alors déduire une expression de k, valide pour tout autre instant :

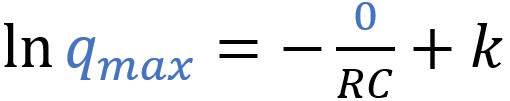
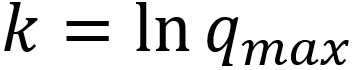L'équation principale peut maintenant être réécrite avec l'expression connue de k, et quelques transformations algébriques permettront d'obtenir une équations générale de la charge en fonction du temps.

Rem. : on utilise les identités « a = ln(e^a) »
           et « ln a + ln b = ln (a·b) ».

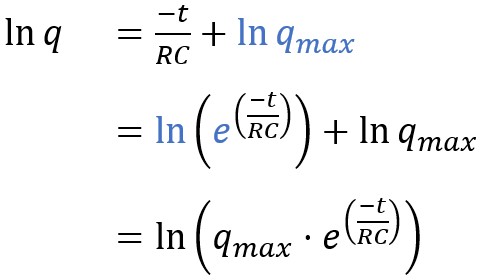Ultimement, l'équation de la charge « restante » en fonction du temps est la suivante :

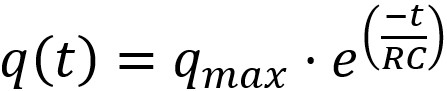Courant de décharge du condensateur

En tout temps, le courant qui décharge le condensateur équivaut au taux de variation de sa charge (négatif si on considère que la valeur du courant est liée à une diminution de la charge) :

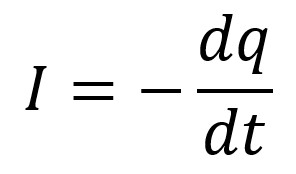La charge q peut être remplacée par l'expression trouvée précédemment. Le courant est donc la dérivée de cette expression par rapport au temps :

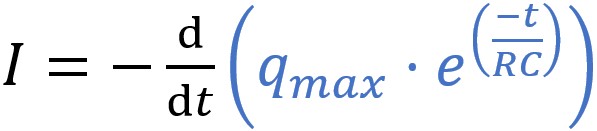
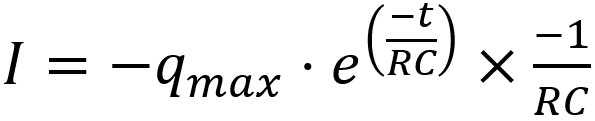
Un réarrangement de l'expression trouvée permet de reconnaître le potentiel initial du condensateur ΔV_Cmax :

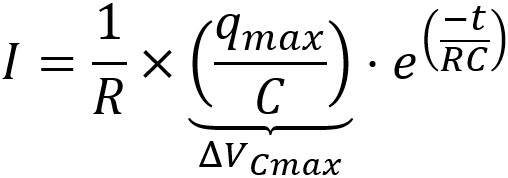
Selon la loi d'Ohm, le rapport « ΔV_Cmax / R » correspond à un courant; c'est donc le courant à l'instant initial, où le potentiel est ΔV_Cmax :

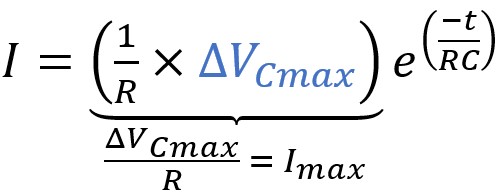
Le courant en fonction du temps est donc donné par l'équation suivante :
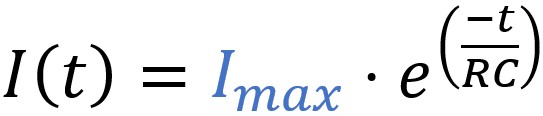