|
Chapitre 6 : Figures et liens
utiles pour la compréhension de la matière
|
|
|
|
|
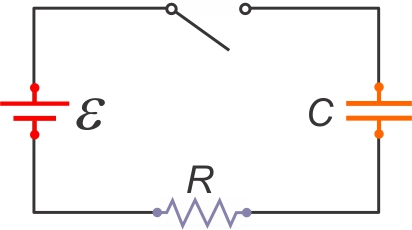
Soit un circuit RC où le condensateur est
initialement vide.
|
|
|
|
|
En fermant l'interrupteur, le condensateur pourra se charger,
mais le courant sera limité par la présence de la résistance et la
charge ne sera pas instantanée.
|
|
|
|
|
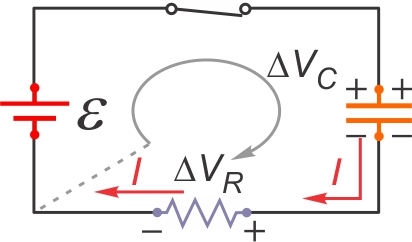
Comme pour le processus de décharge, on peut utiliser l'équation de la maille
unique du circuit, valide à tout instant :
|
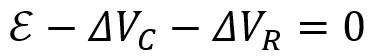
|
|
|
Selon l'équation de la capacité et la loi d'Ohm :
|
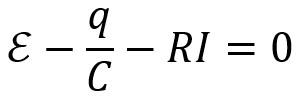
|
|
|
Le courant I représente cette fois-ci le taux de croissance de la
charge par rapport au temps. En équation :
|
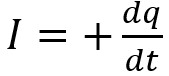
|
|
|
L'équation principale devient :
|
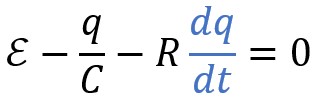
|
|
|
Si on réarrange l'expression pour réunir dq et q
en vue de procéder à une intégration.
On a alors deux intégrales indéfinies :
|
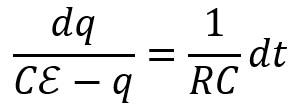
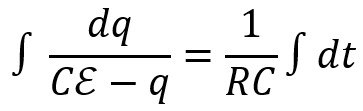
|
|
|
L'intégration des deux termes amène l'expression suivante, où les
deux constantes d'intégration sont réunies dans la même constante
k, dans le terme de droite : |

|
|
|
La constante d'intégration peut être déterminée à partir des
conditions connues pour l'instant initial (t = 0) de la
charge :
À t = 0, la charge est encore nulle : q = 0.
|
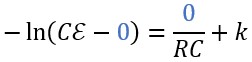
|
|
|
On peut alors déduire une expression de k, valide pour tout
autre instant :
|
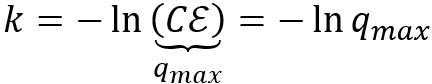
|
|
|
L'équation principale peut maintenant être réécrite avec
l'expression connue de k.
Quelques transformations algébriques permettent ensuite d'obtenir
une équation générale de la charge en fonction du temps.
Rem. : on utilise les identités « a = ln(ea) »,
« ea+b = ea × eb »
et
« ln a + ln b = ln (a·b) ».
|
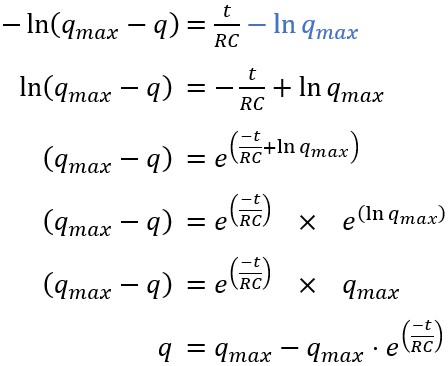
|
|
|
Ultimement, l'équation de la charge accumulée en fonction du temps
est la suivante :
|
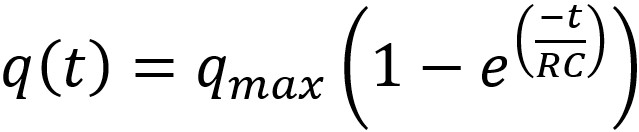
|
|
|
|
Courant de charge du condensateur
En tout temps, le courant qui décharge le condensateur équivaut
au taux de variation de sa charge (positif si on considère que la
valeur du courant est liée à une augmentation de la charge) :
|
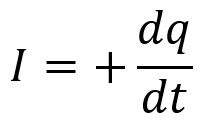
|
|
|
La charge q peut être remplacée par l'expression trouvée
précédemment.
Le courant est donc la dérivée de cette expression par rapport au
temps : |
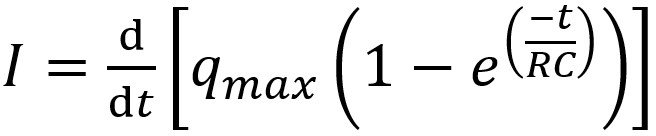
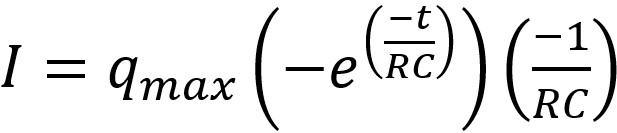
|
|
|
Un réarrangement de l'expression trouvée permet de reconnaître le
potentiel maximal du condensateur, correspondant à celui de la
source.
(Car à la fin de la charge, le courant nul dans les
résistances fait en sorte que la seule chute de potentiel est celle
du condensateur, équivalente à la valeur Ɛ de la source.) |
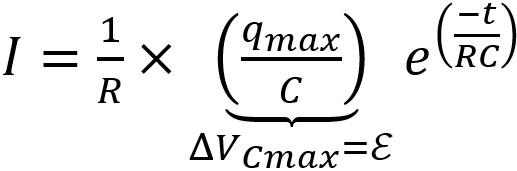
|
|
|
Selon la loi d'Ohm, le rapport « Ɛ / R » correspond à un courant;
c'est le courant maximal Imax, à l'instant
initial, alors que le condensateur vide se comporte comme un
court-circuit et alors que seules la résistance limite le courant : |

|
|
|
Le courant en fonction du temps est donc donné par
l'équation suivante : |

|
|